人教版六年级下册第五单元《数学广角》
《鸽巢问题例1》讲义(教师版)
撰稿人:黄兰梅
| 【教学内容】:人教版六下第五单元P68例1 【教学目标】: 1. 通过操作、观察、比较、说理等数学活动,使学生经历鸽巢问题的形成过程,初步了解鸽巢原理。 2. 会用鸽巢原理解决相关的实际问题或解释相关现象。 【教学重难点】: 理解鸽巢原理,并会运用原理解决简单的实际问题。 |
第一部分:生活中的例子引入(3分钟)

▸ T:请同学们看讲义第一部分,谁能用自己的话说一下这个魔术表演的是什么?
▸ T:这个结论你相信吗?相信的同学请举起手,不相信的同学不举手。
▸ T:我先不揭晓答案,等学完本节课的知识,答案自然就有了。
▸ 请同学们自学讲义第二部分。计时:5分钟。
第二部分:探究抽屉原理(自学5分钟,交流3分钟,汇报8分钟,统整2分钟,共18分钟)
例1:把4个苹果放进3个抽屉中,不管怎么放,总有一个抽屉里至少有2个苹果。
1. “总有”是什么意思? 肯定有,总会有,一定有
“至少”是什么意思?最少,最起码
1. “总有一个抽屉至少有2个苹果”,这个结论正确吗?请你试着说明。
| 贝博士: 解决这个问题,你可以尝试用以下方法: 方法一:动手画一画,分一分,列举出各种情况。 方法二:用假设的方法,先把苹果尽量平均分散放在每个抽屉里。 |
▸学生自学,老师巡视了解情况。
▸学生汇报,老师根据汇报进行追问和统整。
【预设汇报1】:
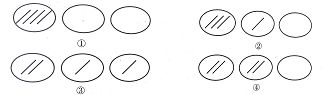
▸师追问:我们来看这种摆法,凭什么说“总有一个抽屉里至少有2个苹果”(第一种摆法有一个抽屉是4个,第二种摆法有一个抽屉是3个,第三种摆法有一个抽屉是2个,第四种摆法有两个抽屉都是2个,所以“总有一个抽屉里至少有2个苹果”)
▸比2个多可以吗?(至少放进2个苹果就是最少是2个,比2个多也是可以的,2个、3个、4个都是符合要求的)
✦师统整:动手摆出所有的可能,发现结果是符合“总有一个抽屉里至少有2个苹果”。
【预设汇报2】:
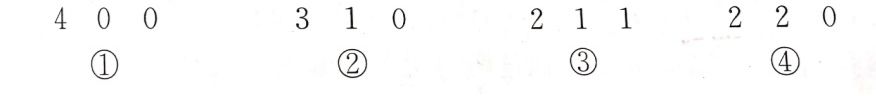
▸师生一起圈出每种分法中不小于2的数,对学生的简洁表示法给予表扬。
▸这两种方法都很好地枚举出了所有摆法,进而验证“总有一个抽屉里至少有2个苹果”的结论是正确的。
▸是不是这样的呢?我们借助洋葱视频再来核对一下。
【预设汇报3】:一共有3个抽屉;如果每个抽屉放1个苹果,一共放了3个;这时还剩1个,无论放到哪个抽屉里,总有一个抽屉至少有 2个苹果。
▸根据生的表达,师同时进行板书图示,引导学生直观认识“这时,无论放到哪个抽屉,那个抽屉就是2个”的情况。
▸师追问:你为什么要先在每个抽屉里放1个呢?(因为总共有4个,平均分,每个抽屉只能分到1个。)
▸ 师追问:你为什么要平均分呢?(板书:平均分)(平均分, 就可以使每个抽屉的笔尽可能少一点, 也就有可能找到和题目意思不一样的情况)
▸师追问:但是这样只能证明总有一个抽屉中肯定会有2个苹果,怎么能证明至少有2个呢?(平均分已经使每个笔筒中的笔尽可能少了, 如果这样都符合要求,那另外的情况肯定也是符合要求了.)
✦师统整:到现在为止,我们可以得出结论,把4个苹果放进3个抽屉中,不管怎么放,总有一个抽屉里至少有2个苹果。。
▸ 师:刚才我们通过不同的方法验证了这句话是正确的。现在老师把题目改一改,你们看看还对不对,完成讲义第三部分。
第三部分:深化抽屉原理(自学3分钟,讨论2分钟,汇报5分钟,共10分钟)
1. 5个苹果放进4个抽屉,总有一个抽屉至少有(2 )个苹果。
2. 10个苹果放进9个抽屉,总有一个抽屉至少有2个苹果。
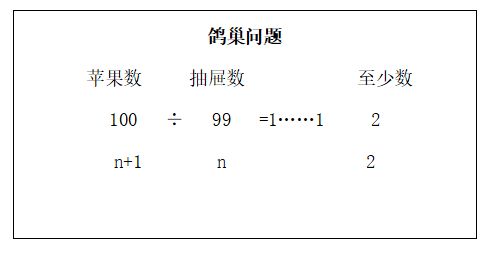
3. 100个苹果放进99个抽屉,总有一个抽屉至少有2个苹果。
想一想:
① 你用哪种方法来解决这几个问题?
你能用算式来说明第3题的结论吗?
② 总结:
观察以上题中数据,当( n+1 )个苹果放进n个抽屉里,总有一个抽屉里至少有( 2)个苹果。
Ø 教师引导学生说理,学生逐渐都采用假设的思路熟练地来表达。
Ø 师:我们为什么都采用假设的方法来分析,而不是画图或举例子呢?(引导学生对两种方法进行比较,体会枚举方法的优越性和局限性,感悟假设方法更具一般性的特点,)
Ø 师:只要苹果的数量比抽屉的数量多1,那么总有一个抽屉至少要放2个苹果。
u 师统整: 像这样的数学问题,我们就叫做“抽屉问题”,又叫“鸽巢问题”,它们里面蕴含的这种数学原理,我们就叫做“鸽巢原理”或“抽屉原理”.(揭题板书)
第四部分:巩固练习(思考2分钟,汇报3分钟,共5分钟)
1. 结合我们本节所学的知识,你能解释一下扑克牌的问题吗?
参考答案: 扑克牌有4种花色,相当于4个抽屉, 5个人相当于5个苹果,如果每个人都各拿一种花色,最后一个人所抽的颜色一定会与前面某一人是相同花色,所以至少有2张牌是同花色的。
2. 5个苹果放进5个抽屉里,总有一个抽屉里至少有几个苹果?为什么?
参考答案: 一共有5个抽屉,如果每个抽屉放一个苹果,刚好放完,所以总有一个抽屉至少有2个苹果。
3. 5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么。
参考答案:一共有3个鸽笼,假设每个鸽笼飞进1只,最多飞进3只,还剩2只鸽子,这两只鸽子可以再平均分到两个鸽笼里,也可以同时飞进一个鸽笼,无论怎么飞,肯定有一个鸽笼里至少有2只鸽子。
第五部分:全课小结(2分钟)
结合本节课的学习目标,说一说你有那些收获?
补充资料:
| 抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄利克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄利克雷原理”。 抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里, 总有一个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”; 另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢,至少飞进2只鸽子,所以也称为 “鸽巢原理”。 |
课外拓展:
| 《晏子春秋》里有一个“二桃杀三士”的故事,晏子采用借“桃”杀人的办法,不费吹灰之力,便达到了他预定的目的,可说是善于运用权谋。值得指出的是,在晏子的权谋之中,包含了一个重要的数学原理——抽屉原理,有兴趣的同学可以了解一下这个典故。 |
板书设计: