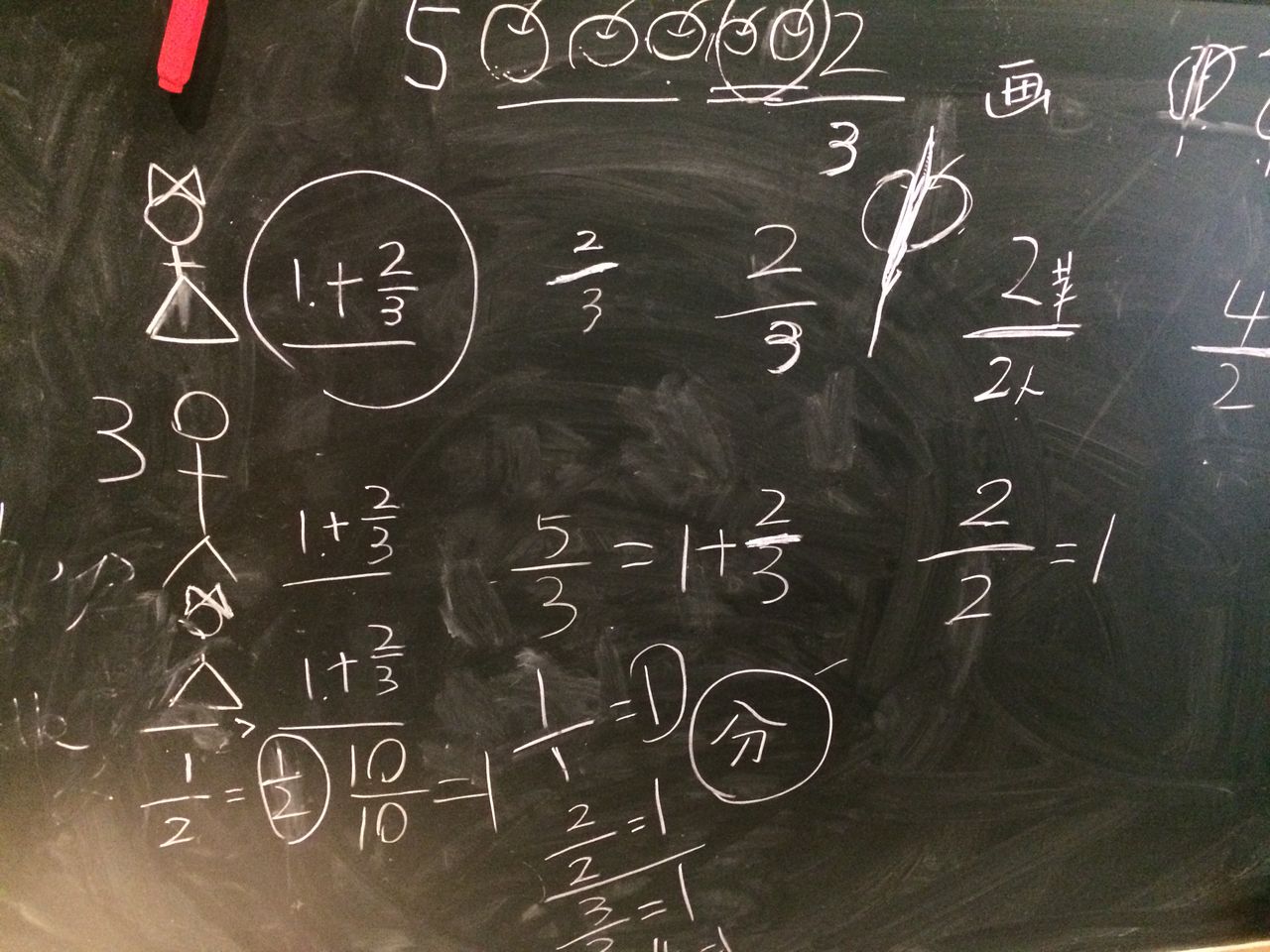
涉及分数时，直接用了两种表达式：16÷3=16/3。毕竟16/3，你可以理解成分数也可以理解成除法的。所以直接一并写了。

除法从某种意义上说就是平均分配。这个含义，上次已经玩过了。

所以今天直接出了几道题，主要是想让他们了解下有关的数学语言、数学符号。

比如那个算式，群里家长说很多三年级孩子都是懵的。

我写出来时，土豆直接把它认成了一个“”厂“”字。就着他这个理解，我直接说有一堆东西，数量是16，堆在厂里等着分配。厂外有3个人等着分这些东西。

那具体要怎么分呢？哦

不需要动脑子的办法，就是先每个人分一个，这样一圈一圈的轮。最后轮5个回合，能把16分完，还余1个。这个办法是可以的，就是效率不高。

那怎么才能效率高一点呢？

让轮着分的次数少一点，效率就提高了。

那怎么才能让轮着分的次数少一点呢，最好少到一两次，甚至只有一次？

这就涉及“估算”，就是要提前估算好几个3接近16。不能超过16，和16一样大当然完美，可以比16小但是最好别小的量超过3（超过3意味着什么？那就意味着至少还可以再分一轮。）

当然，如果已经学会乘法表，那估算起来就简单多了。——3个人分，每人分5个，第一轮就直接分走了15个。当然最后还剩1个。

最后剩下来的这个余数，怎么处理？

可以直接。。。。。，表示余1。

其实最精确、简洁的办法就是写成分数。

于是顺势讲了下分数。

后来发现他对分数的理解不是很好。

就另外拿了一张纸，玩了下分数。哦随便写了个5/7， 问他怎么读的？

5除以7，或者七分之五。

然后轮到他写一个，考我。

他写了个9/6，我一看是一个假分数。于是先按部就班用两种方式读了下：9除以6，或者六分之九。

然后对它做了一些变形。因为他在第一次玩的时候就理解了6/6或其它等位的写法，都是等于1的（看第一张黑板图）。这里算是对这一点的应用。

让他针对1/4+2/4+1/4=1讲个故事，他说买了个披萨，窦老师吃了1块，GiGi抢了2块，给妈妈留了1块，他们3个人就把一整块披萨吃光了，我一块都没吃到。

这个说法，表明他对分数是理解了的。

然后问他5/9的含义，一种就是9里被拿走了5，所以和剩下的4一起，就是完整的9/9，是一整块。

另一种就是5平均分给9个人。这是没办法让获得整分的，所以5/9最精确的表述就是“5均分给9”，具体物理上怎么分割不管。

然后他觉得这个说法有点像耍赖。

我说，但它是最精确的表述。

那么这到底是有什么意义呢？

我稍微想了个故事演绎了下。

有5块糖，9个人拥有对它的平等权利。虽然实际分起来可能难以分得那么精确。但是在理论上，这是要被9均分的5.

有一天，这5颗糖卖了9块钱，于是他们每人分到1块。

有一天，这5颗糖和面粉一起做了90个包子，于是每人分到10个包子。

有一天，这5颗糖被送给了一个很喜欢吃糖的小孩，大家除了帮助别人的喜悦，什么有形的财富都没获得。

......

不管怎么处理，总之这是会被9均分的5。

他对这个说法非常兴奋，但是又说不出所以然来。就是情绪高涨。觉得很好玩。

无法获得整数倍的均分，是除法里一个很大的问题。未完待续。

a/b除法的两层含义：

1)表示总数a均分成b堆，每堆几个？7÷2=7/2

2)表示总数a，每堆b，能分几堆？ 7÷1/2=14