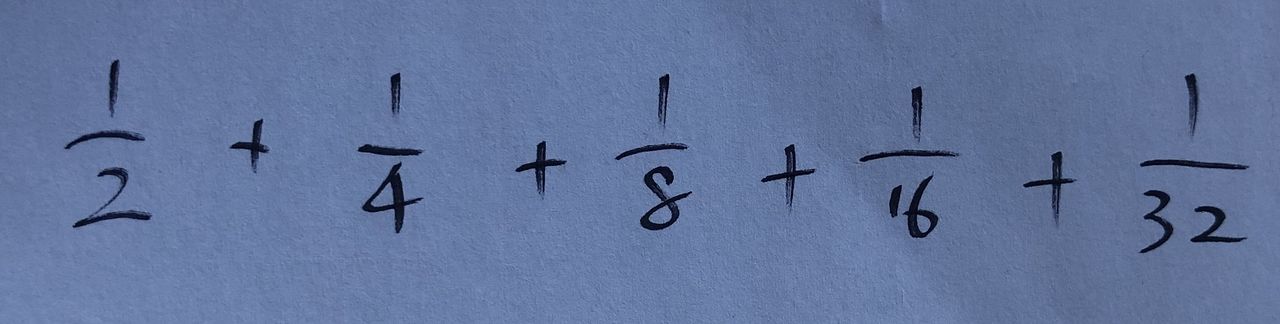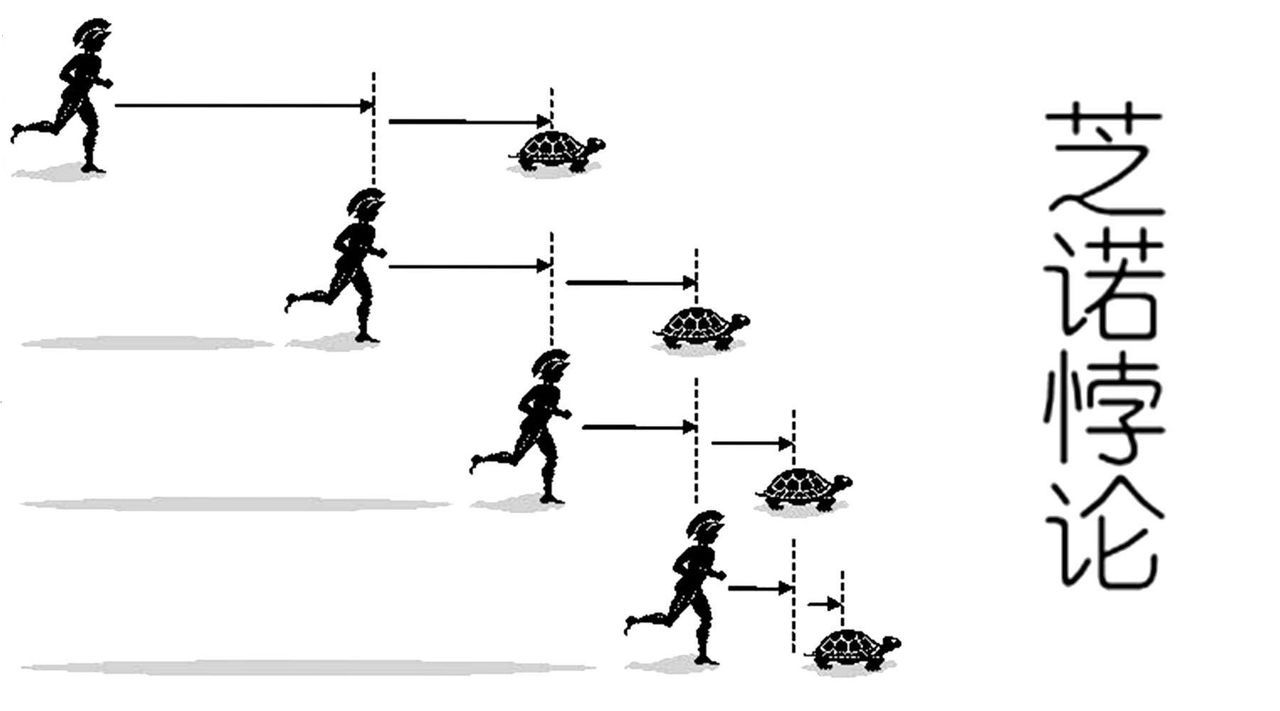
公元前5世纪，芝诺提出了悖论：小乌龟如何跑赢希腊传奇英雄阿喀琉斯？
首先，乌龟先出发，为了追上乌龟，阿喀琉斯必须先跑完乌龟跑过的距离；与此同时，乌龟又前进了一段距离，阿喀琉斯又要跑完这段距离；同时，乌龟又多跑了一段……
逻辑上，这种追逐会永远持续下 去。不管乌龟和阿喀琉斯的距离多近，乌龟总能在阿喀琉斯追赶时多跑一段，意味着阿喀琉斯永远无法超越乌龟
极端地说，这个奇怪的悖论证明了所有运动都是不可能的，但它也说明了有限的东西可以被分割成无限的部分（连续和离散）
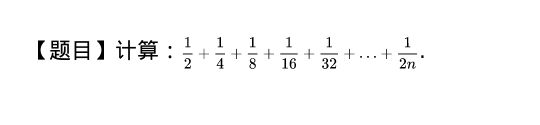
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + ……

你能想到“无穷级数”的概念，在生活中的应用吗？

（比如它通常被用在金融上计算支付贷款，这也是为什么贷款永远还不清的原因！）