数学源自生活,回到思维游戏。
我们今天邀请一位体育老师来带大家探索数学。
| 我们的数学是体育老师教的。是真的。 体育老师说:体育的感染力是那么通透而直接,太适合拿来学数学了。 |
这个女子10000米的比赛,设置了两条起跑线,这又是什么操作。
在中长跑比赛中,我们可以看到套圈的情况出现。根据套圈的位置,我来算算两个人的速度之比吧。
【No.1 田径场上的压轴大戏】

| 4×50米家长接力赛。 我的下一棒是一位陌生的妈妈,虽然看上去身形矫健,但显然没有参与过接力赛事。当我高速冲向她时,她只是站在原地充满期待地看着我,伸着手……这……她真的不害怕吗? 当我确认她一点儿也不会提前启动的时候已经晚了,我几乎直接冲到了她的身上,飞在空中把她推了出去,然后自己来了个就地十八滚。漂亮的摔倒保护的动作。 |
不论是奥运会的田径部分还是专门的田径世锦赛,4×100m接力都是最后的压轴项目。
整理素材的时候不知不觉跟着后续推荐看了好几场。习惯了各种弯弯绕的战术设计,着实错过了不少简单粗暴的激情。
学生们看上去也很少有机会被田径运动所感染,看到那如流水般的交接棒,他们也非常兴奋。
记得博尔特退役一站在4×100m跑道上的悲壮谢幕?

激情过后,来看一些数学问题:
| 1)4×100m是分道跑的,起跑线的位置如何确定?如果只量出每条跑道的宽度可以开始计算了吗? 2)主流的径赛都有哪些项目?它们分别应该在操场的哪个位置起跑,以及分道的原则是什么?这是一个除以400求余数的问题。 3)这个女子10000米的比赛,设置了两条起跑线,这又是什么操作。 4)在中长跑比赛中,我们可以看到套圈的情况出现。根据套圈的位置,我来算算两个人的速度之比吧。 |

伴随着对WR和OR这两个关键字的熟识,学生马上发现了上图中这个耀眼的中国纪录。
顺带着,我们聊起了马家军的故事和举国体制的疯狂……
【No.2 撑杆跳高的杆子有长度限制吗?】
小时候看体育比赛的时候一直有个疑问,撑杆跳高运动员所使用的杆子是每个人都一样吗?如果是自己准备的,那长度方面有没有什么限制?
准备这节课的时候,其实话题是从台球开始构思的,并且最终想到了撑杆跳问题。而台球这件事,又是源自于我在物理期末考试里给学生出的一道题:
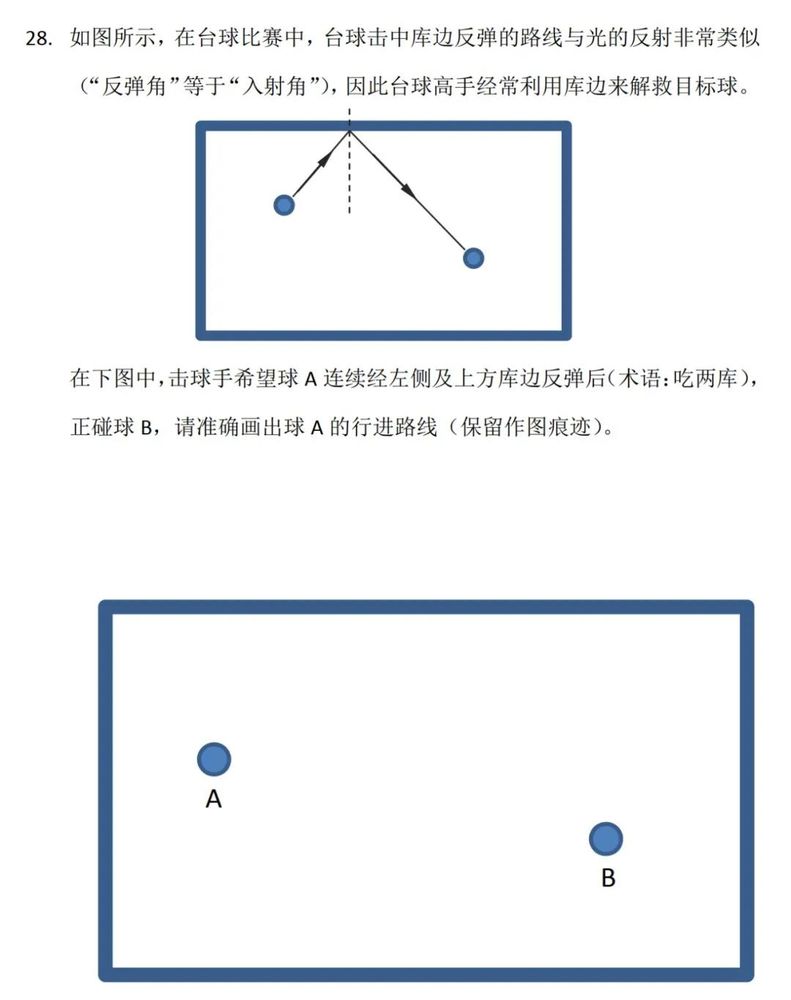
这实际上是一道光学作图题。
我记得小时候在电视上见过一种没有袋的台球比赛,看得我如痴如醉。

先不考虑旋转的问题,这种台球完全就是几何路线的设计。球员每一次击球必须把两个目标球都碰到,而且在碰到第二个目标球之前,母球还必须至少三次撞击库边(有兴趣的话可以以“3 cushion billiards”为关键字搜索视频),人类高手的手感真是让人叹为观止。
看着台球撞来撞去,联想到了撑杆跳的极限。
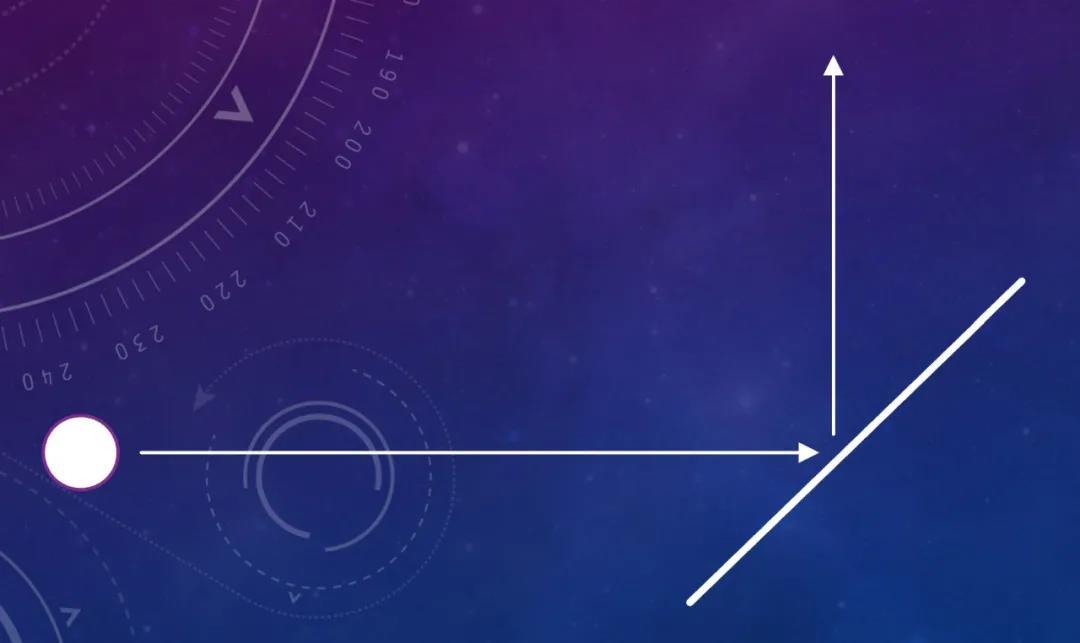
一个小球从左侧冲过来,遇到45°弹性挡板后向上飞起。它能够达到的最大高度就取决于之前的奔跑速度。
撑杆跳比赛中的杆子只是个中介,运动员通过各种技术借助它追求完全的弹性碰撞,争取把动能全部转化为势能。
所以,既然有动能的限制,那么即便你抡个10m长的杆子也应该无法把自己扔到10m的高度上吧?

从水平转向垂直是个相对简单的模型,再歪一些,便是跳远和投掷项目的助跑和出手角度问题。
虽然小学高年级的数学能力尚不足以准确算出这些事,但影响因素和定性判断是完全可以建立的。
【No.3 运动与图线】
在奥数的世界里,行程问题是一个重头戏,相遇、追及,不过是各种各样的赛跑。在面对这些问题的时候,画图的能力常常比计算更加重要。
甲的速度是5.5m/s,乙的速度是3.3m/s,他们从同一个地方出发沿相反方向沿100m长的操场匀速绕圈。他们的第100次相遇会在哪里?
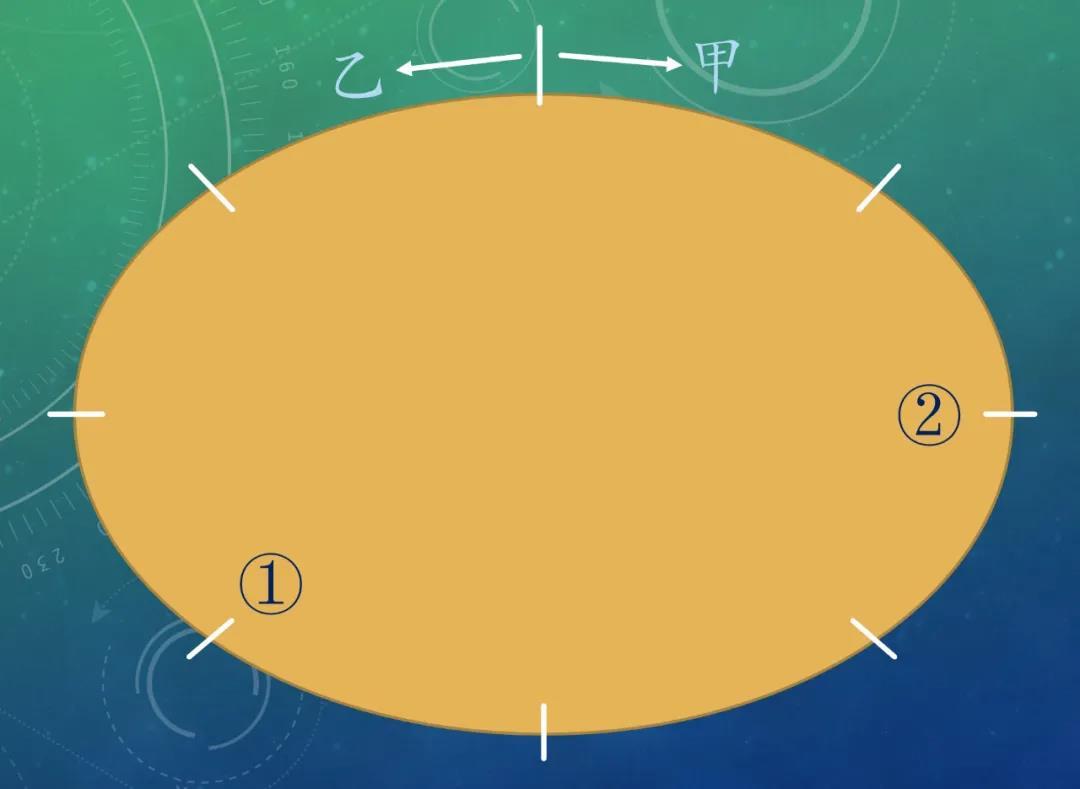
5.5和3.3只是个幌子,简化为5:3之后,就在八分圆圈上点点儿找规律就行了。
除了用来做题的图线,折线图还能表达故事情节。比如,把传统龟兔赛跑的故事用v-t图和s-t图表现出来,或者,自己在横纵坐标上重新设计一个惊心动魄的情节。
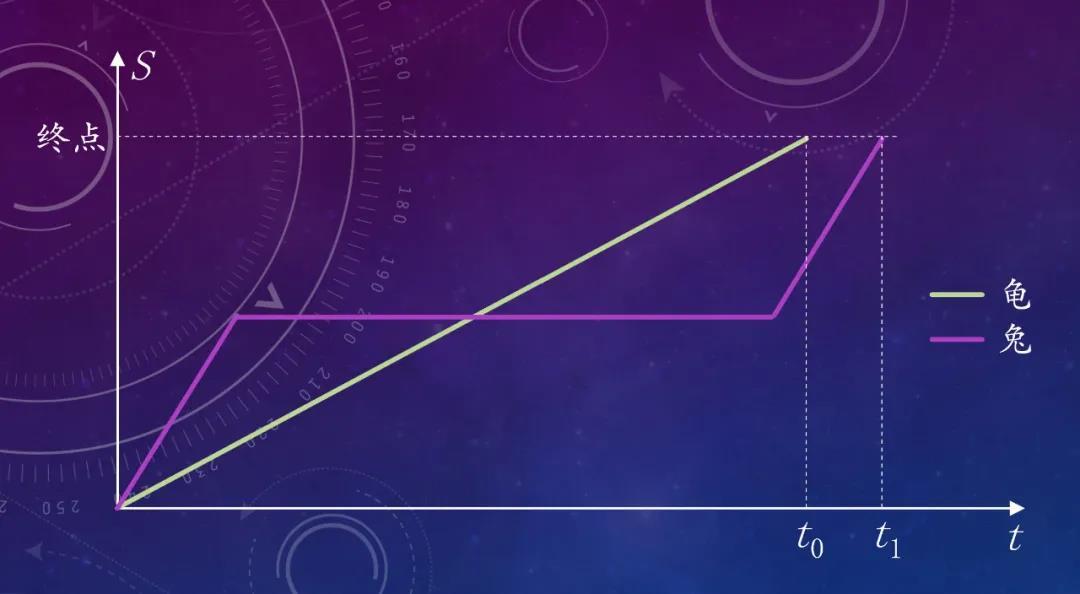
还有一种图不是那么直观,但也诠释了“有图有真相”的道理。
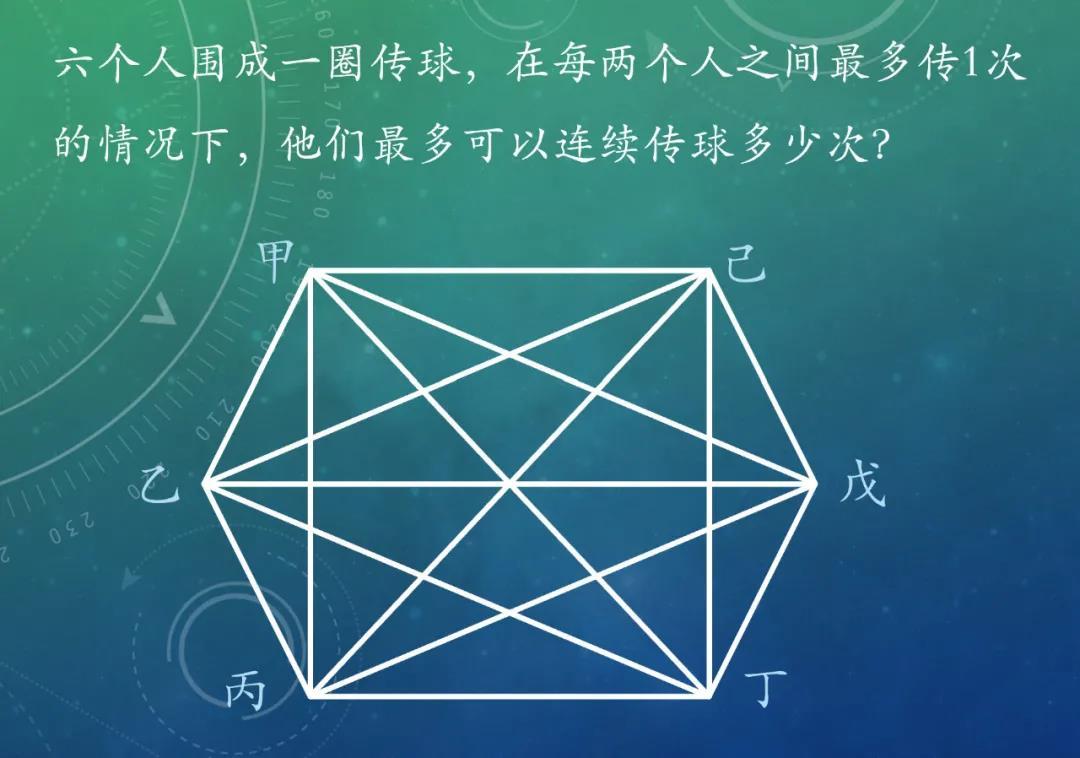
这个班上有高手,听完题,马上就列出了5+4+3+2+1的算式。但是,这15次传球可以连起来吗?这实际上是一个“一笔画”问题,也就是看这个图形是否可以一笔画出来。如果不行的话,去掉几根线就可以了呢?
【No.4 方块棋盘上的惊喜】
上到这一节有一个重大惊喜。
自从将方块棋引入围棋教学以来,第一天、第一次玩儿就能先手下赢我的学生终于出现了,这个学习能力着实惊人!
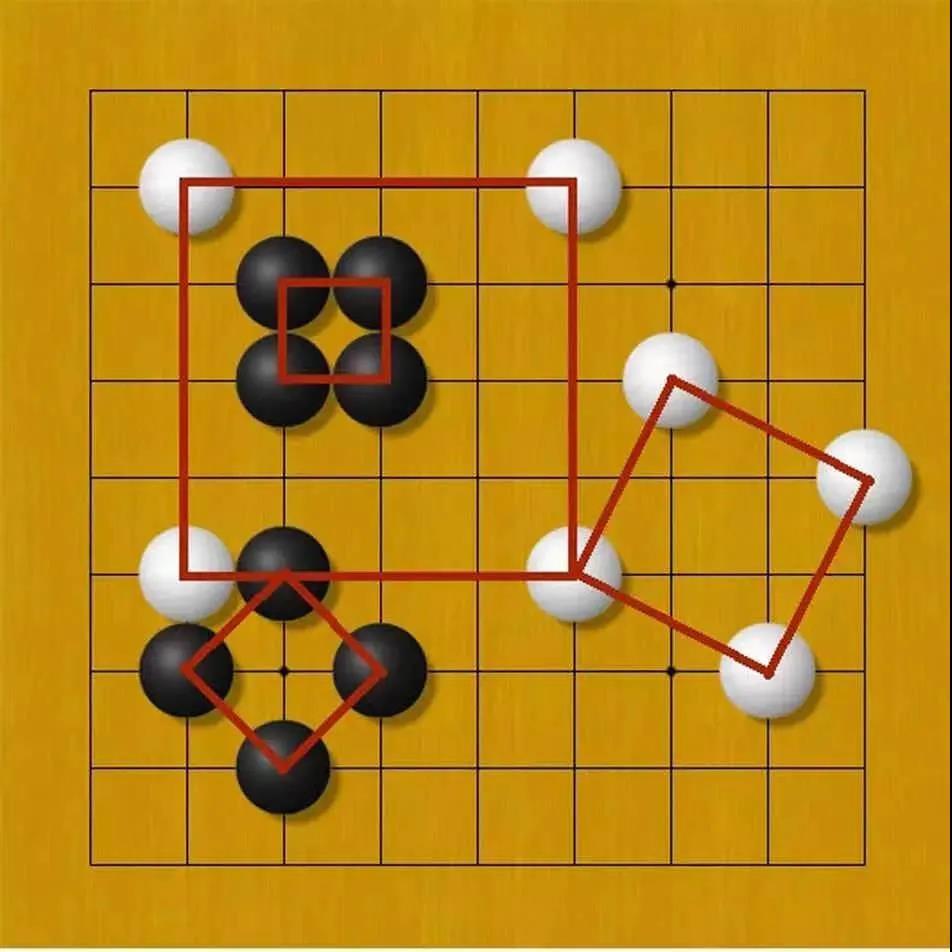
那么,如果每个棋格的面积是1,上面这几个正方形的面积各是多少?在一个5×5的小棋盘上,又能摆出多少种面积不同的正方形呢?
既然涉及到棋格上的面积问题,摆弄摆弄点阵是少不了的。学生们也很惊讶,大家一起推出来的公式竟然真的好用。
在各种主流棋类中,五子棋无疑是启蒙用时最短、上手最快的。但是由于先手优势过大,竞技五子棋又变成了冗长规则的代言人。
为了让正式的五子棋比赛能够开展起来,日本人付出了巨大的努力。先后手的问题是下节课的内容,我们先研究一下棋盘上的对称问题。
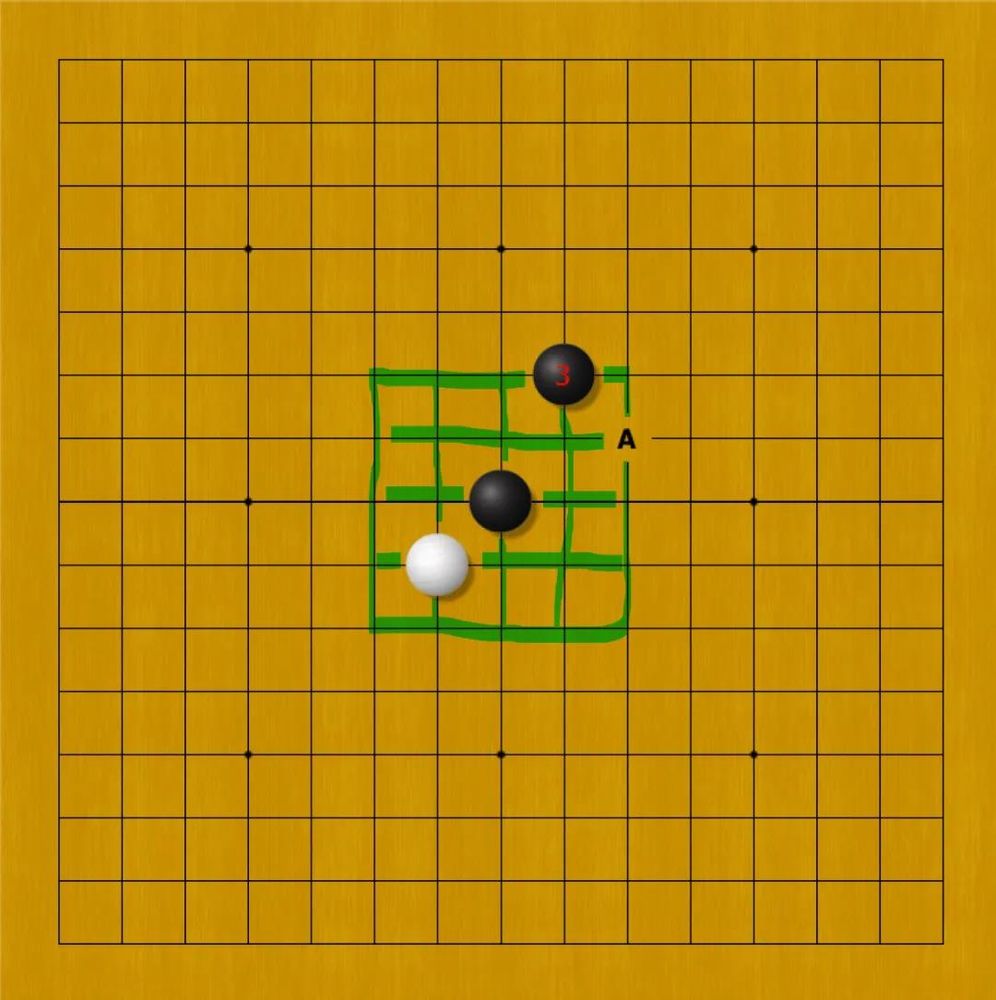
按照日本人拟定的五子棋规则,开局第一手必须落于棋盘中央,第二手必须挨着第一手(直挨或者斜挨都可以),第三手必须落于中间5×5的区域之内。三手完成便确立了一种开局,且拥有名字。图中所示为“明月局”。
显见,如果第三手落于A处,形势完全一样,应该还是“明月局”。那么日本五子棋规则下,一共有多少种不同的开局呢?
【No.5 先手优势与公平的规则】
我作为一个围棋爱好者,很少去了解AI在别的棋界都整了些什么名堂。在研究国际象棋的先手优势时,偶然看到了一个熟悉的名字——AlphaZero。
围棋的英文是Go,这给搜索相关资料带来了巨大的不便。AlphaGo有几个版本。最初的AlphaGo是输入了人类高手的棋谱之后,再自我提升的。进阶版AlphaGoZero没有输入人类棋谱,而是从零开始自我修炼。再进阶的版本AlphaZero里已经没有Go了,告诉它任何对弈规则,它都可以马上开始修炼,并在几个小时之后成为顶尖高手。

AlphaZero在和国际象棋传统AI程序StockFish的100盘对抗中,执白先手25胜25平,执黑后手3胜47平,保持不败的同时诠释了先手的力道。
相比之下,围棋因为目标不像连五、擒王那么直截了当,所以有了先手贴目的余地,这种公平性也是它的一大卖点。可惜,明明贴6目是比较合适的,规则里非要贴6.5,而中国规则又不得不贴7.5,这又是什么逻辑、怎么回事呢?

下棋中的先手,放到球类运动里就是“发球”,其先手优势(或劣势)也不可回避,每个项目都需要针对自己的特点去解决。
比如说增加比赛局数,3局2胜、5局3胜、7局4胜……你知道有些比赛因为偶然性太大,竟然要搞到35局18胜吗?
先手劣势的也有,比如说排球。八十年代女排风光无限,至今宋世雄那句“17比18,换发球,18比17”言犹在耳。当时的排球和羽毛球,都是只有发球方才有资格得分,胶着的时候,光剩下换发球了,比赛长度非常不可控。

对先后手的体验,小学数学有专门的“游戏题”:桌上10个小球,两个人轮流拿取,每人每次拿1~2个,先手和后手谁有必胜策略?如何获胜?
以上题面,每个参数都可以调整。比如桌上100个小球,每次拿2~5个,谁拿到最后一个谁输……
【No.6 这是个真实的积分榜吗?】
4个队踢循环赛,一共是几场比赛?如果胜一场得3分,平一场得1分,负一场不得分,当四个队的全部比赛进行完之后,积分榜有可能是下面这个样子吗?
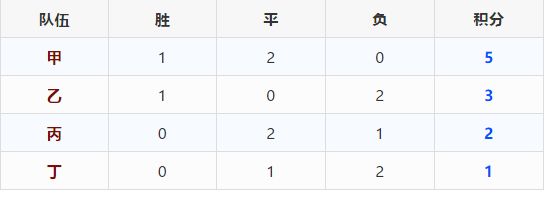
我们这种每天浸淫在足球世界里的人,感觉这些问题都实在不是问题,但现场的几位大人都没有看出问题,最终问题还是被头脑开放的小孩子们七嘴八舌地发现了。
体育赛事的组织形式是个很大的话题,我这几年也是饱受各种情况的困扰,一个业余赛事想坚持办下来真的不容易。别说业余了,贵为世界杯,每次也有很多棘手的话题要讨论。
上次世界杯预选赛,亚洲区的比赛有过一个40进12的阶段。如果让你来规划这个比赛过程,你会采用什么样的赛制呢?
前两年我做班主任的时候,煽动学生组织比赛是我的一大爱好,其中有一个赛事我印象颇为深刻,即用扑克牌算24点和36点。
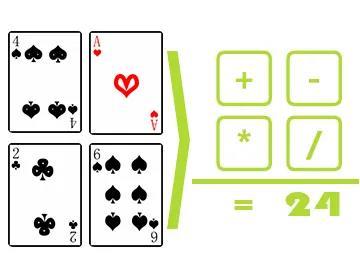
为了能够捉对pk,比赛需要合适的人数,为此,他们先设计了预选赛:在数学课上,用大屏幕打出随机数,所有同学奋笔疾书,之后前7名进入淘汰赛。
为什么是前7呢,因为他们斗志昂扬,执意要给我一个种子选手的免选资格。但是,他们又忌惮我作为数学老师的实力,怎么办呢?
每场我参加的比赛都要附加三名裁判:一名帮我翻牌(别人都是自己翻),另一名捂住我的眼睛,还有一名计时7秒。这7秒就是我先修数学30年的先手优势贴目补偿。